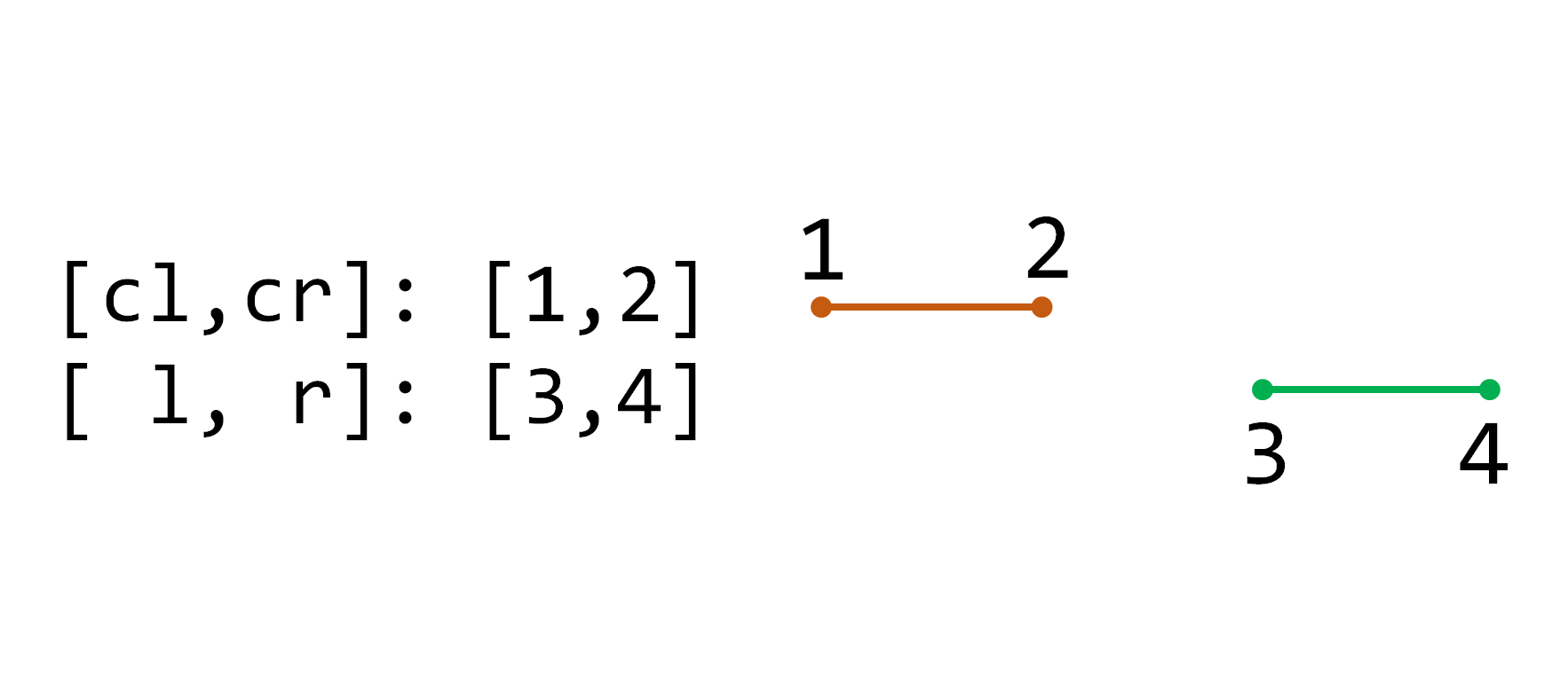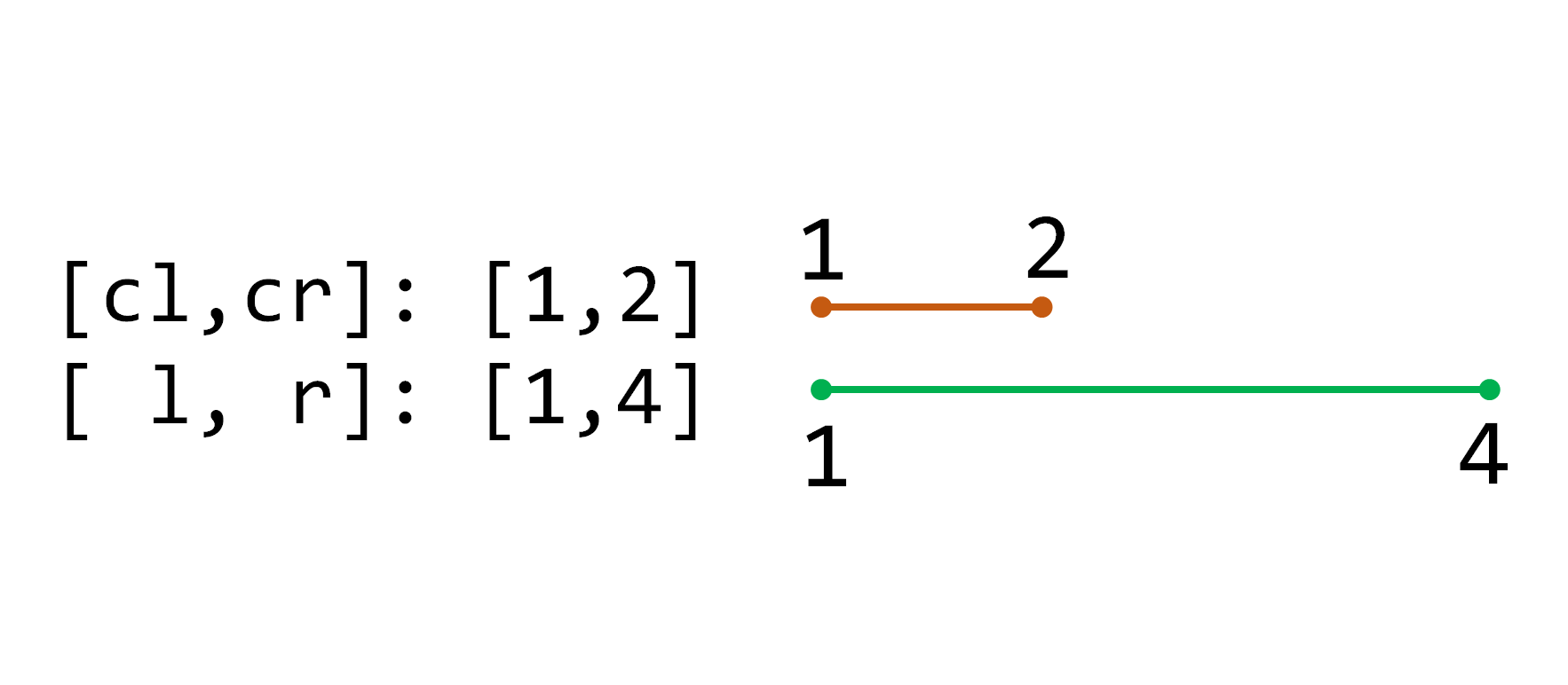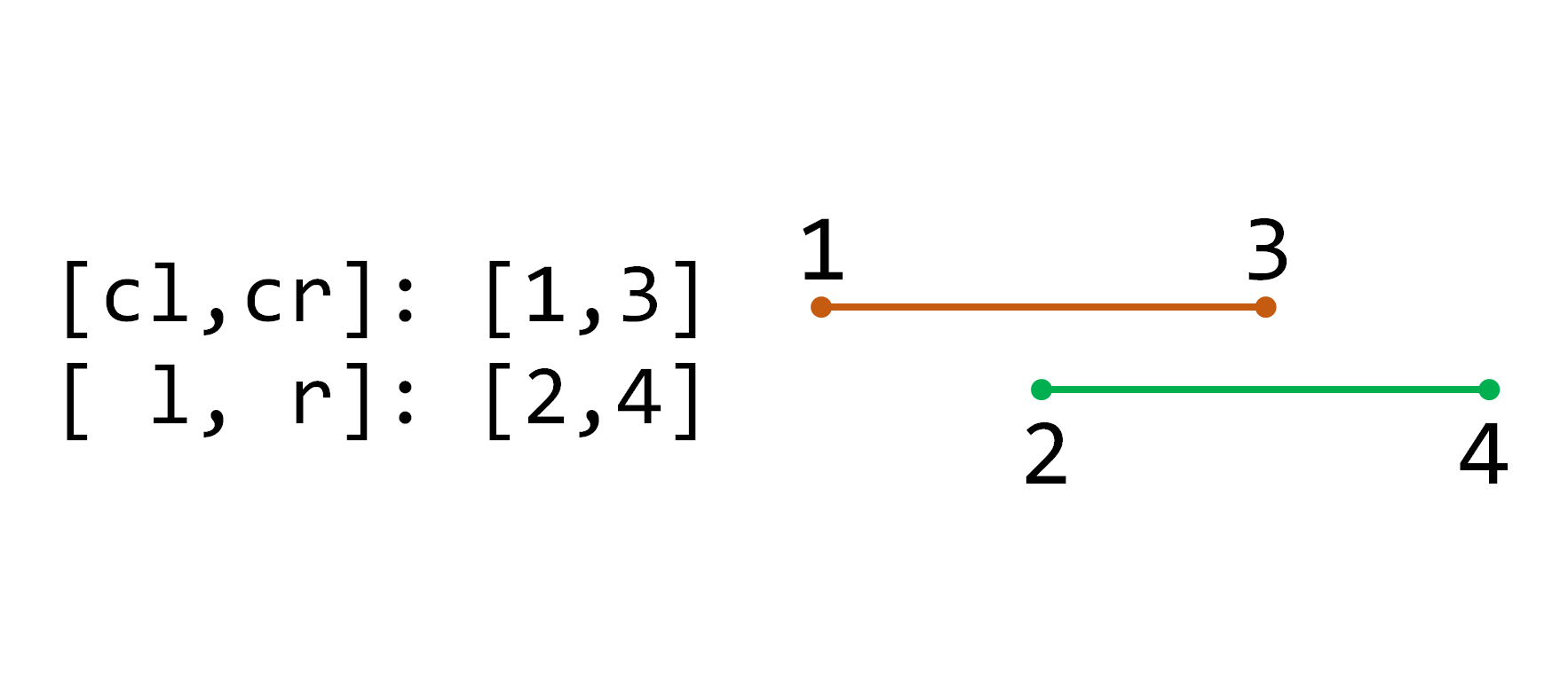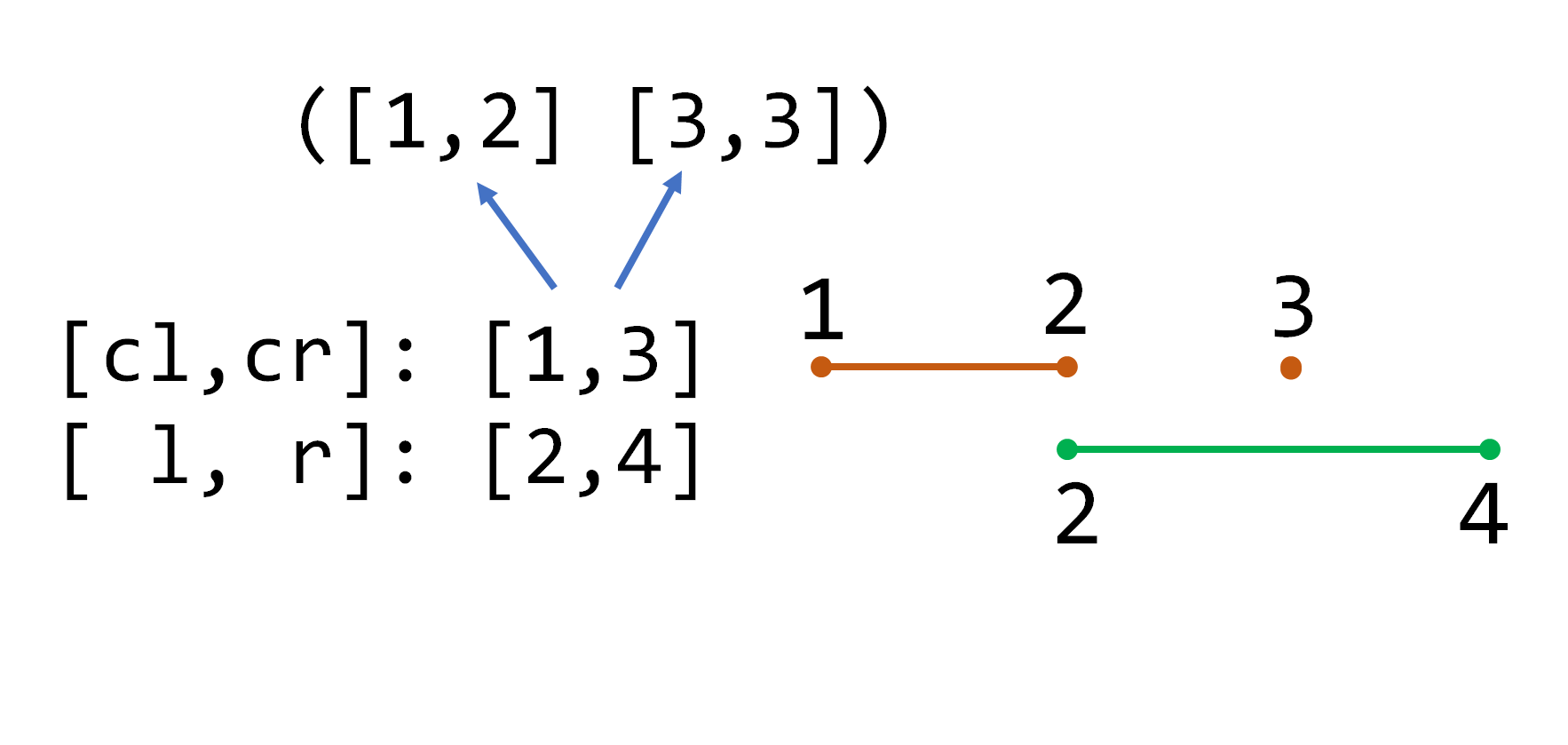线段树
线段树(Segment Tree)几乎是算法竞赛最常用的数据结构了,它主要用于维护区间信息(要求满足结合律)。与树状数组相比,它可以实现 O(log n) 的区间修改,还可以同时支持多种操作(加、乘),更具通用性。
接下来我们用这道模板题为例,看看线段树是怎么维护区间和这一信息的。
(洛谷P3372 【模板】线段树 1)
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.求出某区间每一个数的和
输入格式
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式
输出包含若干行整数,即为所有操作2的结果。
线段树的建立
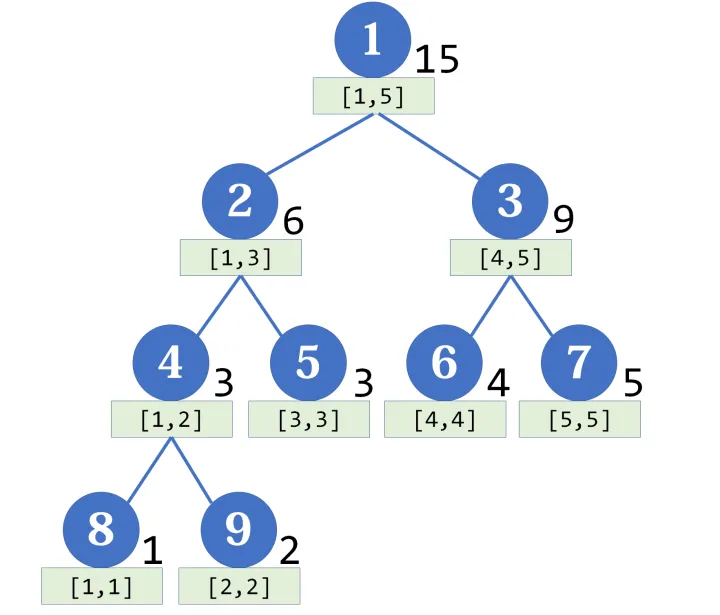
线段树是一棵平衡二叉树。母结点代表整个区间的和,越往下区间越小。注意,线段树的每个节点都对应一条线段(区间),但并不保证所有的线段(区间)都是线段树的节点,这两者应当区分开。
如果有一个数组[1,2,3,4,5],那么它对应的线段树大概长这个样子:
每个节点 p 的左右子节点的编号分别为 2p 和 2p+1 ,假如节点 p 储存区间 [a,b] 的和,设mid=⌊(a+b)/2⌋ ,那么两个子节点分别储存 [a, mid] 和 [mid+1,b] 的和。可以发现,左节点对应的区间长度,与右节点相同或者比之恰好多1。
如何从数组建立一棵线段树?我们可以考虑递归地进行。
void build(ll l = 1, ll r = n, ll p = 1)
{
if (l == r) // 到达叶子节点
tree[p] = A[l]; // 用数组中的数据赋值
else
{
ll mid = (l + r) / 2;
build(l, mid, p * 2); // 先建立左右子节点
build(mid + 1, r, p * 2 + 1);
tree[p] = tree[p * 2] + tree[p * 2 + 1]; // 该节点的值等于左右子节点之和
}
}
我这里用一张gif展现上述的过程:
区间修改
在讲区间修改前,要先引入一个“懒标记”(或延迟标记)的概念。懒标记是线段树的精髓所在。对于区间修改,朴素的想法是用递归的方式一层层修改(类似于线段树的建立),但这样的时间复杂度比较高。使用懒标记后,对于那些正好是线段树节点的区间,我们不继续递归下去,而是打上一个标记,将来要用到它的子区间的时候,再向下传递。
代码比较复杂,我慢慢解释:
void update(ll l, ll r, ll d, ll p = 1, ll cl = 1, ll cr = n)
{
if (cl > r || cr < l) // 区间无交集
return; // 剪枝
else if (cl >= l && cr <= r) // 当前节点对应的区间包含在目标区间中
{
tree[p] += (cr - cl + 1) * d; // 更新当前区间的值
if (cr > cl) // 如果不是叶子节点
mark[p] += d; // 给当前区间打上标记
}
else // 与目标区间有交集,但不包含于其中
{
ll mid = (cl + cr) / 2;
mark[p * 2] += mark[p]; // 标记向下传递
mark[p * 2 + 1] += mark[p];
tree[p * 2] += mark[p] * (mid - cl + 1); // 往下更新一层
tree[p * 2 + 1] += mark[p] * (cr - mid);
mark[p] = 0; // 清除标记
update(l, r, d, p * 2, cl, mid); // 递归地往下寻找
update(l, r, d, p * 2 + 1, mid + 1, cr);
tree[p] = tree[p * 2] + tree[p * 2 + 1]; // 根据子节点更新当前节点的值
}
}
更新时,我们是从最大的区间开始,递归向下处理。注意到,任何区间都是线段树上某些节点的并集。于是我们记目标区间为 [l,r] ,当前区间为 [cl,cr] , 当前节点为 p ,我们会遇到三种情况:
\1. 当前区间与目标区间没有交集:
这时直接结束递归。
2.当前区间被包括在目标区间里:
这时可以更新当前区间,别忘了乘上区间长度:
tree[p] += (cr - cl + 1) * d;
然后打上懒标记(叶子节点可以不打标记,因为不会再向下传递了):
mark[p] += d;
这个标记表示“该区间上每一个点都要加上d”。因为原来可能存在标记,所以是+=而不是=。
3.当前区间与目标区间相交,但不包含于其中:
这时把当前区间一分为二,分别进行处理。如果存在懒标记,要先把懒标记传递给子节点(注意也是+=,因为原来可能存在懒标记):
ll mid = (cl + cr) / 2;
mark[p * 2] += mark[p];
mark[p * 2 + 1] += mark[p];
两个子节点的值也就需要相应的更新(后面乘的是区间长度):
tree[p * 2] += mark[p] * (mid - cl + 1);
tree[p * 2 + 1] += mark[p] * (cr - mid);
不要忘记清除该节点的懒标记:
mark[p] = 0;
这个过程并不是递归的,我们只往下传递一层(所以叫“懒”标记啊!),以后要用再才继续传递。其实我们常常把这个传递过程封装成一个函数:
inline void push_down(ll p, ll len)
{
mark[p * 2] += mark[p];
mark[p * 2 + 1] += mark[p];
tree[p * 2] += mark[p] * (len - len / 2);
tree[p * 2 + 1] += mark[p] * (len / 2); // 右边的区间可能要短一点
mark[p] = 0;
}
然后在update函数中这样调用:
push_down(p, cr - cl + 1);
传递完标记后,再递归地去处理左右两个子节点。
下面的gif显示了为区间 [1,4] 加上1的过程:
至于单点修改,只需要令左右端点相等即可。
区间查询
有了区间修改的经验,区间查询的方法完全类似,直接上代码了:
ll query(ll l, ll r, ll p = 1, ll cl = 1, ll cr = n)
{
if (cl > r || cr < l)
return 0;
else if (cl >= l && cr <= r)
return tree[p];
else
{
ll mid = (cl + cr) / 2;
push_down(p, cr - cl + 1);
return query(l, r, p * 2, cl, mid) + query(l, r, p * 2 + 1, mid + 1, cr);
// 上一行拆成三行写就和区间修改格式一致了
}
}
一样的递归,一样自顶至底地寻找,一样的合并信息。
本文只介绍了最基本的线段树用法,其实线段树的题目千奇百怪,有很多技巧。在维护不同的信息时,需要注意是否需要乘区间长度、不同的标记之间是否相互影响等。最后附上模板题的完整代码:
#include <bits/stdc++.h>
#define MAXN 100005
using namespace std;
typedef long long ll;
inline ll read()
{
ll ans = 0;
char c = getchar();
while (!isdigit(c))
c = getchar();
while (isdigit(c))
{
ans = ans * 10 + c - '0';
c = getchar();
}
return ans;
}
ll n, m, A[MAXN], tree[MAXN * 4], mark[MAXN * 4]; // 经验表明开四倍空间不会越界
inline void push_down(ll p, ll len)
{
mark[p * 2] += mark[p];
mark[p * 2 + 1] += mark[p];
tree[p * 2] += mark[p] * (len - len / 2);
tree[p * 2 + 1] += mark[p] * (len / 2);
mark[p] = 0;
}
void build(ll l = 1, ll r = n, ll p = 1)
{
if (l == r)
tree[p] = A[l];
else
{
ll mid = (l + r) / 2;
build(l, mid, p * 2);
build(mid + 1, r, p * 2 + 1);
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
}
void update(ll l, ll r, ll d, ll p = 1, ll cl = 1, ll cr = n)
{
if (cl > r || cr < l)
return;
else if (cl >= l && cr <= r)
{
tree[p] += (cr - cl + 1) * d;
if (cr > cl)
mark[p] += d;
}
else
{
ll mid = (cl + cr) / 2;
push_down(p, cr - cl + 1);
update(l, r, d, p * 2, cl, mid);
update(l, r, d, p * 2 + 1, mid + 1, cr);
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
}
ll query(ll l, ll r, ll p = 1, ll cl = 1, ll cr = n)
{
if (cl > r || cr < l)
return 0;
else if (cl >= l && cr <= r)
return tree[p];
else
{
ll mid = (cl + cr) / 2;
push_down(p, cr - cl + 1);
return query(l, r, p * 2, cl, mid) + query(l, r, p * 2 + 1, mid + 1, cr);
}
}
int main()
{
n = read();
m = read();
for (int i = 1; i <= n; ++i)
A[i] = read();
build();
for (int i = 0; i < m; ++i)
{
ll opr = read(), l = read(), r = read();
if (opr == 1)
{
ll d = read();
update(l, r, d);
}
else
printf("%lld\n", query(l, r));
}
return 0;
}
(2021年更新)
这篇文章是一年多前写的,当时的代码给人感觉很啰嗦,这里给一个紧凑的新版本(区间加,区间求和):
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int MAXN = 1e5 + 5;
ll tree[MAXN << 2], mark[MAXN << 2], n, m, A[MAXN];
void push_down(int p, int len)
{
if (len <= 1) return;
tree[p << 1] += mark[p] * (len - len / 2);
mark[p << 1] += mark[p];
tree[p << 1 | 1] += mark[p] * (len / 2);
mark[p << 1 | 1] += mark[p];
mark[p] = 0;
}
void build(int p = 1, int cl = 1, int cr = n)
{
if (cl == cr) return void(tree[p] = A[cl]);
int mid = (cl + cr) >> 1;
build(p << 1, cl, mid);
build(p << 1 | 1, mid + 1, cr);
tree[p] = tree[p << 1] + tree[p << 1 | 1];
}
ll query(int l, int r, int p = 1, int cl = 1, int cr = n)
{
if (cl >= l && cr <= r) return tree[p];
push_down(p, cr - cl + 1);
ll mid = (cl + cr) >> 1, ans = 0;
if (mid >= l) ans += query(l, r, p << 1, cl, mid);
if (mid < r) ans += query(l, r, p << 1 | 1, mid + 1, cr);
return ans;
}
void update(int l, int r, int d, int p = 1, int cl = 1, int cr = n)
{
if (cl >= l && cr <= r) return void(tree[p] += d * (cr - cl + 1), mark[p] += d);
push_down(p, cr - cl + 1);
int mid = (cl + cr) >> 1;
if (mid >= l) update(l, r, d, p << 1, cl, mid);
if (mid < r) update(l, r, d, p << 1 | 1, mid + 1, cr);
tree[p] = tree[p << 1] + tree[p << 1 | 1];
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = 1; i <= n; ++i)
cin >> A[i];
build();
while (m--)
{
int o, l, r, d;
cin >> o >> l >> r;
if (o == 1)
cin >> d, update(l, r, d);
else
cout << query(l, r) << '\n';
}
return 0;
}
实际上线段树还可以维护区间最值、区间gcd等等,操作除了区间加也可以是区间乘、区间赋值,了解原理后很容易改。
原文链接